Spotlight

Spotlight Articles

Articles that are representative of our research interests
Spotlight
Image: Adobe Stock

SQL Algorithms

Python Code vs SQL Code

Image: Mark Blacher

SQL is the standard language for retrieving and manipulating relational data. Although SQL is ubiquitous for simple analytical queries, it is rarely used for more complex computations in, for instance, machine learning, linear algebra, and other computationally-intensive algorithms. These algorithms are often implemented in procedural languages, which are very different from declarative SQL. However, SQL actually does provide constructs to perform general computations. We have shown how to translate procedural constructs that are used in other languages to SQL, which enables SQL-only implementations of complex algorithms. Using SQL for algorithms keeps computations close to the data, requires minimal user permissions, and increases software portability. The performance of the resulting SQL algorithms depends heavily on the underlying database system and the SQL code. To our surprise, it turned out that query engines like HyPer can be highly performant and in some cases even outperform state-of-the-art implementations of standard machine learning methods like logistic regression.

Publications:

Code repository: GitHubExternal link

Convexity Certificates from Hessians

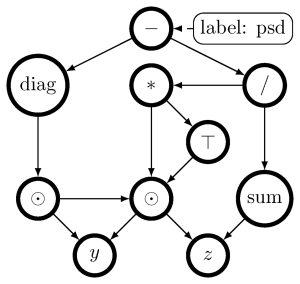
PSD expression template

Image: Julien Klaus

The Hessian of a differentiable convex function is positive semidefinite. Therefore, checking the Hessian of a given function is a natural approach to certify convexity. However, implementing this approach is not straightforward, since it requires a representation of the Hessian that allows its analysis. Here, we implement this approach for a class of functions that is rich enough to support classical machine learning. For this class of functions, we show how to compute computational graphs of their Hessians and how to check these graphs for positive-semidefiniteness. We compare our implementation of the Hessian approach with the well-established disciplined convex programming (DCP) approach and prove that the Hessian approach is at least as powerful as the DCP approach for differentiable functions. Furthermore, we show for a state-of-the-art implementation of the DCP approach that, for differentiable functions, the Hessian approach is actually more powerful, that is, it can certify the convexity of a larger class of differentiable functions.

Publications:

  •  P. Rump, N. Merk, J. Klaus, M. Wenig and J. Giesen. Convexity Certificates for Symbolic Tensor Expressions. Proceedings of the 33d International Joint Conference on Artificial Intelligence (IJCAI), (2024)
  • J. Klaus, N. Merk, K. Wiedom, S. Laue and J. Giesen. Convexity Certificates from Hessians. Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS), (2022) (arXiv versionExternal link)

Model Counting and Sampling via Semiring Extensions

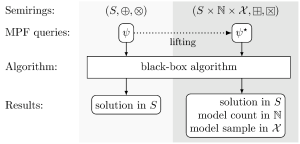
Semiring extension

Illustration: Andreas Goral

Many decision and optimization problems have natural extensions as counting problems. The best known example is the Boolean satisfiability problem (SAT), where we want to count the satisfying assignments of truth values to the variables, which is known as the #SAT problem. Likewise, for discrete optimization problems, we want to count the states on which the objective function attains the optimal value. Both SAT and discrete optimization can be formulated as selective marginalize a product function (MPF) queries. We have shown how general selective MPF queries can be extended for model counting. MPF queries are encoded as tensor hypernetworks over suitable semirings that can be solved by generic tensor hypernetwork contraction algorithms. Our model counting extension is again an MPF query, on an extended semiring, that can be solved by the same contraction algorithms. Model counting is required for uniform model sampling. We have shown how the counting extension can be further extended for model sampling by constructing yet another semiring. We have implemented the model counting and sampling extensions. Experiments show that our generic approach is competitive with the state of the art in model counting and model sampling.

Publication:

  • A. Goral, J. Giesen, M. Blacher, C. Staudt and J. Klaus. Model Counting and Sampling via Semiring Extensions. Proceedings of the 38d AAAI Conference on Artificial Intelligence (AAAI), (2024) 

Symbolic Regression

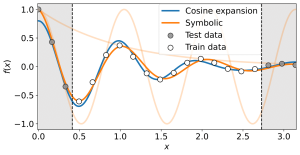
Symbolische Regression

Image: Paul Kahlmeyer

In a regression task, a function is learned from labeled data to predict the labels at new data points. The goal is to achieve small prediction errors. In symbolic regression, the goal is more ambitious, namely, to learn an interpretable function that makes small prediction errors. This additional goal largely rules out the standard approach used in regression, that is, reducing the learning problem to learning parameters of an expansion of basis functions by optimization. Instead, symbolic regression methods search for a good solution in a space of symbolic expressions. To cope with the typically vast search space, most symbolic regression methods make implicit, or sometimes even explicit, assumptions about its structure. We argue that the only obvious structure of the search space is that it contains small expressions, that is, expressions that can be decomposed into a few subexpressions. We show that systematically searching spaces of small expressions finds solutions that are more accurate and more robust against noise than those obtained by state-of-the-art symbolic regression methods. In particular, systematic search outperforms state-of-the-art symbolic regressors in terms of its ability to recover the true underlying symbolic expressions on established benchmark data sets.

Publication:

  • P. Kahlmeyer, J. Giesen, M. Habeck and H. Voigt.  Scaling Up Unbiased Search-based Symbolic Regression. Proceedings of the 33d International Joint Conference on Artificial Intelligence (IJCAI), (2024)

Why Capsule Neural Networks Do Not Scale

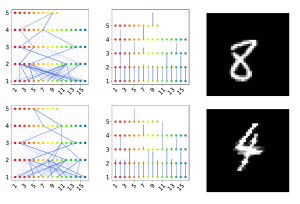
Two examples of parse-trees

Image: Matthias Mitterreiter

Capsule neural networks replace simple, scalar-valued neurons with vector-valued capsules. They are motivated by the pattern recognition system in the human brain, where complex objects are decomposed into a hierarchy of simpler object parts. Such a hierarchy is referred to as a parse-tree. Conceptually, capsule neural networks have been defined to mimic this behavior. The capsule neural network (CapsNet), by Sabour, Frosst, and Hinton, is the first actual implementation of the conceptual idea of capsule neural networks. CapsNets achieved state-of-the-art performance on simple image recognition tasks with fewer parameters and greater robustness to affine transformations than comparable approaches. This sparked extensive follow-up research. However, despite major efforts, no work was able to scale the CapsNet architecture to more reasonable-sized datasets. We provide a reason for this failure and argue that it is most likely not possible to scale CapsNets beyond toy examples. In particular, we show that the concept of a parse-tree, the main idea behind capsule neuronal networks, is not present in CapsNets. We also show theoretically and experimentally that CapsNets suffer from a vanishing gradient problem that results in the starvation of many capsules during training.

Publication:

  • M. Mitterreiter, M. Koch, J. Giesen and S. Laue. Why Capsule Neural Networks Do Not Scale: Challenging the Dynamic Parse-Tree Assumption. Proceedings of the 37th AAAI Conference on Artificial Intelligence (AAAI), (2023) 9209-9216

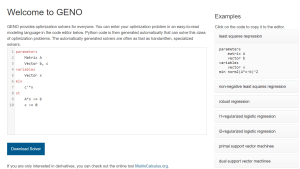
GENeric Optimization

Screenshot GENO

Screenshot GENO

Image: Julien Klaus

Optimization problems are ubiquitous in science, engineering, economics, and especially in machine learning. Traditionally, their efficient solution requires the implementation of customized and optimized solvers. Implementing and tuning a specialized solver can take weeks or even months. With GENOExternal link we dramatically speed up the development process for continuous optimization problems without sacrificing the efficiency of the solvers. GENO automatically generates solvers for almost any continuous optimization problem. It consists of a simple yet flexible modeling language, a symbolic differentiation module for vector and matrix expressions (MatrixcalculusExternal link), and a generic solver that makes use of the symbolic derivatives.

Publications:

Funding: The GENO project has been funded by Deutsche Forschungsgemeinschaft (DFG)External link within the priority program Algorithms for Big Data (SPP 1736)External link and under the grant LA 2971/1-1.

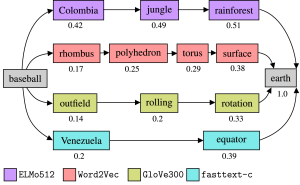
Routing in Wikipedia Graphs

Routing paths for different word embeddings

Image: Paul Kahlmeyer

Deep learning models for different natural language processing (NLP) tasks often rely on pre-trained word embeddings, that is, vector representations of words. Therefore, it is crucial to evaluate pre-trained word embeddings independently of downstream tasks. Such evaluations try to assess whether the geometry induced by a word embedding captures connections made in natural language, such as, analogies, clustering of words, or word similarities. Here, traditionally, similarity is measured by comparison to human judgment. However, explicitly annotating word pairs with similarity scores by surveying humans is expensive. We tackle this problem by formulating a similarity measure that is based on an agent for routing the Wikipedia hyperlink graph. In this graph, word similarities are implicitly encoded by edges between articles. We show on the English Wikipedia that our measure correlates well with a large group of traditional similarity measures, while covering a much larger proportion of words and avoiding explicit human labeling. Moreover, since Wikipedia is available in more than 300 languages, our measure can easily be adapted to other languages, in contrast to traditional similarity measures.

Publication:

Code repository: GitHubExternal link

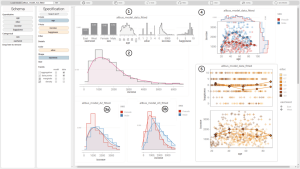
Visual Analytics for Probabilistic Programming

Lumen in action

Lumen in action

Image: Philipp Lucas

Probabilistic programming is a powerful means for formally specifying machine learning models. The inference engine of a probabilistic programming environment can be used for serving complex queries on these models. Most of the current research in probabilistic programming is dedicated to the design and implementation of highly efficient inference engines. Much less research aims at making the power of these inference engines accessible to non-expert users. Probabilistic programming means writing code. Yet, many potential users from promising application areas such as the social sciences lack programming skills. This prompted recent efforts in synthesizing probabilistic programs directly from data. However, working with synthesized programs still requires the user to read, understand, and write some code, for instance, when invoking the inference engine for answering queries. Therefore, we have designed and implemented an interactive visual approach to synthesizing and querying probabilistic programs that does not require the user to read or write code.

Publications:

Code repository: GitHubExternal link

Vectorized Sorting of Primitive Types

Compare and Exchange Module

Image: Mark Blacher

Sorting is a fundamental problem in computer science. Sorting algorithms are part of numerous applications in both commercial and scientific environments. So far, most implementations of sorting algorithms like  Quicksort do not take advantage of vector instruction sets, which are an integral part of modern CPUs. One reason for that is that the vectorization of sorting algorithms is a cumbersome task, since existing sorting algorithms cannot be directly expressed in SIMD instructions. We have introduced new vectorization techniques for sorting networks and Quicksort that allow to design faster, more robust, and memory efficient sorting algorithms for primitive types like int and float. Based on these techniques, we have implemented a sorting algorithm with AVX2 vector instructions that outperforms general purpose sorting implementations and competing high-performance implementations for these primitive types.

Publications:

Social media: Vectorized sorting on Hacker NewsExternal link and on Google's Open Source BlogExternal link

Code repository: GitHubExternal link

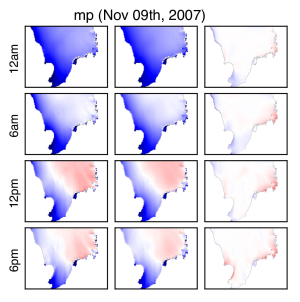
Sparse + Low Rank Models

North Sea floods caused by cyclone Tilo

Image: Frank Nussbaum

General multivariate probability distributions are typically intractable. Here, intractability means two things. First, the distributions cannot be learned efficiently from data, and second, inference queries like computing a most probable element of the sample space on which the probability distribution is defined cannot be answered efficiently. A main reason for intractability is that the distributions' numbers of parameters are too large. (Conditional) independencies among the different dimensions of the sample space can significantly reduce the number of parameters, since (conditional) independencies among the dimensions can be realized by setting parameters or groups of parameters to zero. Models with many parameters set to zero are called sparse. If the sparsity signifies conditional indepencies, then the model is also called a graphical model, since the independencies can be summarized in a graph on the dimensions. Another means of reducing the number of model parameters are low rank structures of matrices that describe interactions among the dimensions. Low rank essentially means that singular values become zero, that is, low rank is also realized by some form of sparsity which also known as rank sparsity. Models that exhibit both forms of sparsity are called sparse + low rank. We have designed efficient algorithms for learning sparse + low rank models with statistical guarantees, as well as efficient inference algorithms.

Publications:

Code repository: GitHubExternal link

Mixed Membership Gaussians

Top five images for five topics

Image: Paul Kahlmeyer

Prototypical mixed membership models like the latent Dirichlet allocation (LDA) topic model use only simple discrete features. However, state-of-the-art representations of images, text, and other modalities are given by continuous feature vectors. Therefore, we have studied Gaussian mixed membership models that work on continuous feature vectors. In these models, each observation is a mixture of Gaussians and, as in LDA, the mixing proportions are drawn from a Dirichlet distribution.  Mixed membership Gaussians are different from classical Gaussian mixture models, where the mixing proportions are fixed, and each individual observation is from a single Gaussian component. Thus, the mixture in Gaussian mixture models is, in contrast to mixed membership Gaussians, only over several observations. We have shown that the parameters of  Gaussian mixed membership models can be learned efficiently and effectively by Pearson’s method of moments.

Publications:

Programming Contests

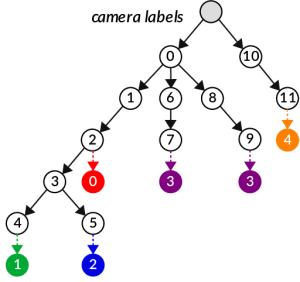
Camera labels for competition

Image: Mark Blacher

Mark Blacher won the 2019 ACM SIGMOD programming contest that asked the participants to sort 10, 20, and 60 GB of data on a given machine that could not fit the larger data sets into its main memory. Therefore, the larger data sets required smart solutions for fast incremental reading of the data from the file system and writing the sorted result back. Mark Blacher did so in his implementation by adapting Mergesort  to the specific hardware that was used in the contest.

In 2020 Mark Blacher, Julien Klaus, and Matthias Mitterreiter won the ACM SIGMOD programming contest again. In this year, the challenge was an entity resolution task, namely, the identification of product specifications of cameras and camera equipment from multiple e-commerce websites that represent the same product. It quickly turned out that standard methods based on unsupervised learning were too slow for the given task. Hence, an alternative approach that uses mock labels was developed. Mock labels are sets of strings that are used to represent real-world entities. The mock labels were created from the training data and used in the resolution step. This approach achieved significantly faster resolution than the competing approaches by other top ranked teams. Since all the top ranked teams had achieved the same quality score for the solution, the speed of resolution was used to decide the winner.

Publication: